Scilab: Root Locus, Transfer Function Analysis

昨天考完控工...結論是...又爆了一次...
最後一題 Root Locus還畫錯= =|

所以，今天就來說一下怎麼用 Scilab畫 Root Locus，題目就是昨天寫錯的那一題。

Problem

Transfer Function

題目沒給，也不需要

Characteristic Equation

1 + KL(s) = 0
L(s)=(s+5)^2 / s^3

Solve in Scilab

要建立"s"的多項式，一個好方法是：先產生一個只有一個根在0的多項式，也就是 s。
s = poly(0, "s"); //s 是以"s"為變數名稱，只有一個根在 0 的多項式
然後再用 s來產生更複雜的多項式。

以本題來說，就是：
L = (s+5)^2 / s^3

如何？簡單吧= =
接下來需要將多項式轉換成線性系統(Linear System)，我還沒研究好這是什麼...
sysL = syslin('c',L)
'c' 是連續的意思(continuous system)

接下來就可以畫圖了，只要一個指令：
evans(sysL, 50)
50是指畫到 K=50，可以任意更改。

如果你覺得圖怪怪的，那你有認真唸書。怪在實數軸跟虛數軸的單位長度不同，要打開圖形選項中 Aspect標籤裡的 isoview選項即可。

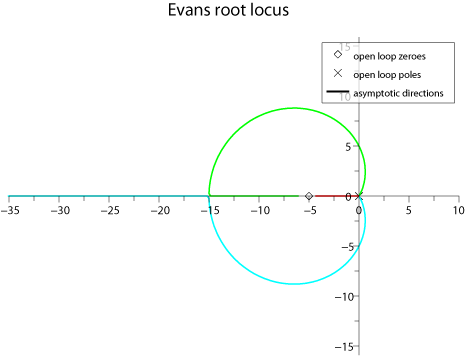
And...

我們也可以畫 Bode, Nyquist, Nichols 等圖形，方法如下：

Bode Plot

Assume that L(s) is a transfer function.
bode(sysL)

Nyquist

nyquist(sysL)

Nichols

black(L)
//誰能告訴我為何叫 black?
//還有 Nichols Plot 是什麼我也不知道XD

Scilab 複數運算

因為今天把工程計算機借給了某評審，導致我回家沒計算機用，事前沒想到會這樣...所以就打開Scilab來算啦！試了好久，做一下筆記。

表示虛數的 i, j，在 Scilab中用%i表示，首先要知道這個。

舉個例，我們要算某 Transfer Function T= R/[R + 1/(sC)]

令 R= 4.7KΩ, C= 0.01μF，並令 s= jω求 f= 1kHz的 Frenquency Response，這樣在Scilab中的算式就是：
T=4700./(4700+1./(%i.*2.*%pi.*1e3.*0.01e-6))

接著算Transfer Function的相移(複數平面的角度)，用atan()函數來算：
atan(imag(T),real(T))

換算成度數：
atan(imag(T),real(T)).*360./%pi

atan()的第一個參數是虛數部份，第二個才是實數，要注意。real()跟imag()就是取實部跟虛部的意思。